Wavelet Tutorial - Part 4

by Robi Polikar

Multiresolution Analysis: The Discrete Wavelet Transform

Why is the Discrete Wavelet Transform Needed?

Although the discretized continuous wavelet transform enables the computation of the continuous wavelet transform by computers, it is not a true discrete transform. As a matter of fact, the wavelet series is simply a sampled version of the CWT, and the information it provides is highly redundant as far as the reconstruction of the signal is concerned. This redundancy, on the other hand, requires a significant amount of computation time and resources. The discrete wavelet transform (DWT), on the other hand, provides sufficient information both for analysis and synthesis of the original signal, with a significant reduction in the computation time.

The DWT is considerably easier to implement when compared to the CWT. The basic concepts of the DWT will be introduced in this section along with its properties and the algorithms used to compute it. As in the previous chapters, examples are provided to aid in the interpretation of the DWT.

The Discrete Wavelet Transform (DWT)

The foundations of the DWT go back to 1976 when Croiser, Esteban, and Galand devised a technique to decompose discrete time signals. Crochiere, Weber, and Flanagan did a similar work on coding of speech signals in the same year. They named their analysis scheme as subband coding. In 1983, Burt defined a technique very similar to subband coding and named it pyramidal coding which is also known as multiresolution analysis. Later in 1989, Vetterli and Le Gall made some improvements to the subband coding scheme, removing the existing redundancy in the pyramidal coding scheme. Subband coding is explained below. A detailed coverage of the discrete wavelet transform and theory of multiresolution analysis can be found in a number of articles and books that are available on this topic, and it is beyond the scope of this tutorial.

The Subband Coding and The Multiresolution Analysis

The main idea is the same as it is in the CWT. A time-scale representation of a digital signal is obtained using digital filtering techniques. Recall that the CWT is a correlation between a wavelet at different scales and the signal with the scale (or the frequency) being used as a measure of similarity. The continuous wavelet transform was computed by changing the scale of the analysis window, shifting the window in time, multiplying by the signal, and integrating over all times. In the discrete case, filters of different cutoff frequencies are used to analyze the signal at different scales. The signal is passed through a series of high pass filters to analyze the high frequencies, and it is passed through a series of low pass filters to analyze the low frequencies.

The resolution of the signal, which is a measure of the amount of detail information in the signal, is changed by the filtering operations, and the scale is changed by upsampling and downsampling (subsampling) operations. Subsampling a signal corresponds to reducing the sampling rate, or removing some of the samples of the signal. For example, subsampling by two refers to dropping every other sample of the signal. Subsampling by a factor n reduces the number of samples in the signal n times.

Upsampling a signal corresponds to increasing the sampling rate of a signal by adding new samples to the signal. For example, upsampling by two refers to adding a new sample, usually a zero or an interpolated value, between every two samples of the signal. Upsampling a signal by a factor of n increases the number of samples in the signal by a factor of n.

Although it is not the only possible choice, DWT coefficients are usually sampled from the CWT on a dyadic grid, i.e., $s_0 = 2$ and $t_0 = 1$, yielding $s = 2^{\, j}$ and $t = k \cdot 2^{\, j}$, as described in Part 3. Since the signal is a discrete time function, the terms function and sequence will be used interchangeably in the following discussion. This sequence will be denoted by x[n], where n is an integer.

The procedure starts with passing this signal (sequence) through a half band digital lowpass filter with impulse response h[n]. Filtering a signal corresponds to the mathematical operation of convolution of the signal with the impulse response of the filter. The convolution operation in discrete time is defined as follows:

$x[n] * h[n] = \sum\limits_{k = -\infty}^\infty x[k] \cdot h[n - k]$

Equation 4.1

A half band lowpass filter removes all frequencies that are above half of the highest frequency in the signal. For example, if a signal has a maximum of 1000 Hz component, then half band lowpass filtering removes all the frequencies above 500 Hz.

The unit of frequency is of particular importance at this time. In discrete signals, frequency is expressed in terms of radians. Accordingly, the sampling frequency of the signal is equal to 2p radians in terms of radial frequency. Therefore, the highest frequency component that exists in a signal will be p radians, if the signal is sampled at Nyquist's rate (which is twice the maximum frequency that exists in the signal); that is, the Nyquist's rate corresponds to p rad/s in the discrete frequency domain. Therefore using Hz is not appropriate for discrete signals. However, Hz is used whenever it is needed to clarify a discussion, since it is very common to think of frequency in terms of Hz. It should always be remembered that the unit of frequency for discrete time signals is radians.

After passing the signal through a half band lowpass filter, half of the samples can be eliminated according to the Nyquist's rule, since the signal now has a highest frequency of $\frac{p}{2}$ radians instead of p radians. Simply discarding every other sample will subsample the signal by two, and the signal will then have half the number of points. The scale of the signal is now doubled. Note that the lowpass filtering removes the high frequency information, but leaves the scale unchanged. Only the subsampling process changes the scale. Resolution, on the other hand, is related to the amount of information in the signal, and therefore, it is affected by the filtering operations. Half band lowpass filtering removes half of the frequencies, which can be interpreted as losing half of the information. Therefore, the resolution is halved after the filtering operation. Note, however, the subsampling operation after filtering does not affect the resolution, since removing half of the spectral components from the signal makes half the number of samples redundant anyway. Half the samples can be discarded without any loss of information. In summary, the lowpass filtering halves the resolution, but leaves the scale unchanged. The signal is then subsampled by 2 since half of the number of samples are redundant. This doubles the scale.

This procedure can mathematically be expressed as

$y[n] = \sum\limits_{k = -\infty}^\infty h[k] \cdot x[2n - k]$

Equation 4.2

Having said that, we now look how the DWT is actually computed: The DWT analyzes the signal at different frequency bands with different resolutions by decomposing the signal into a coarse approximation and detail information. DWT employs two sets of functions, called scaling functions and wavelet functions, which are associated with low pass and highpass filters, respectively. The decomposition of the signal into different frequency bands is simply obtained by successive highpass and lowpass filtering of the time domain signal. The original signal x[n] is first passed through a halfband highpass filter g[n] and a lowpass filter h[n]. After the filtering, half of the samples can be eliminated according to the Nyquist's rule, since the signal now has a highest frequency of $\frac{p}{2}$ radians instead of p . The signal can therefore be subsampled by 2, simply by discarding every other sample. This constitutes one level of decomposition and can mathematically be expressed as follows:

$y_{high}[k] = \sum\limits_{n} x[n] \cdot g[2k - n]$

$y_{low}[k] = \sum\limits_{n} x[n] \cdot h[2k - n]$

Equation 4.3

where $y_{high}[k]$ and $y_{low}[k]$ are the outputs of the highpass and lowpass filters, respectively, after subsampling by 2.

This decomposition halves the time resolution since only half the number of samples now characterizes the entire signal. However, this operation doubles the frequency resolution, since the frequency band of the signal now spans only half the previous frequency band, effectively reducing the uncertainty in the frequency by half. The above procedure, which is also known as the subband coding, can be repeated for further decomposition. At every level, the filtering and subsampling will result in half the number of samples (and hence half the time resolution) and half the frequency band spanned (and hence double the frequency resolution). Figure 4.1 illustrates this procedure, where x[n] is the original signal to be decomposed, and h[n] and g[n] are lowpass and highpass filters, respectively. The bandwidth of the signal at every level is marked on the figure as "f".

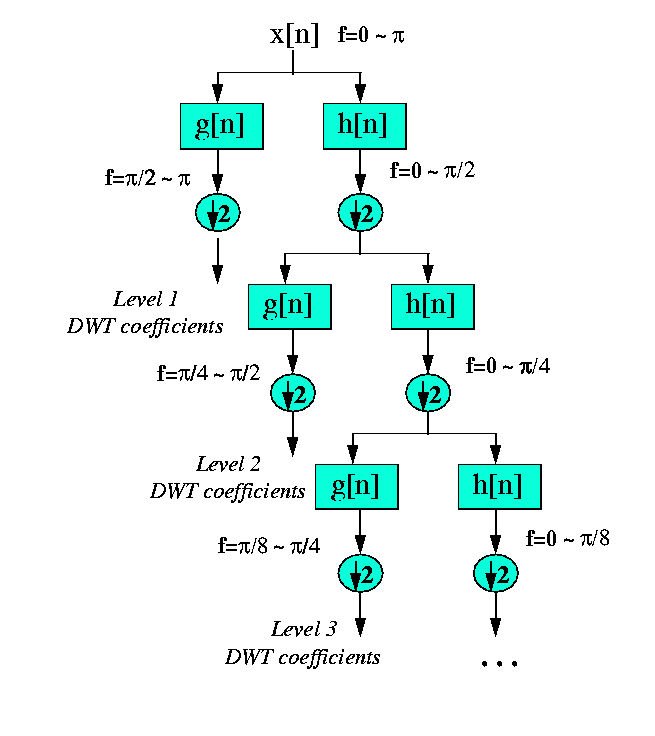
Figure 4.1 The Subband Coding Algorithm

As an example, suppose that the original signal x[n] has 512 sample points, spanning a frequency band of zero to p rad/s. At the first decomposition level, the signal is passed through the highpass and lowpass filters, followed by subsampling by 2. The output of the highpass filter has 256 points (hence half the time resolution), but it only spans the frequencies $\frac{p}{2}$ to p rad/s (hence double the frequency resolution). These 256 samples constitute the first level of DWT coefficients. The output of the lowpass filter also has 256 samples, but it spans the other half of the frequency band, frequencies from 0 to $\frac{p}{2}$ rad/s. This signal is then passed through the same lowpass and highpass filters for further decomposition. The output of the second lowpass filter followed by subsampling has 128 samples spanning a frequency band of 0 to $\frac{p}{4}$ rad/s, and the output of the second highpass filter followed by subsampling has 128 samples spanning a frequency band of $\frac{p}{4}$ to $\frac{p}{2}$ rad/s. The second highpass filtered signal constitutes the second level of DWT coefficients. This signal has half the time resolution, but twice the frequency resolution of the first level signal. In other words, time resolution has decreased by a factor of 4, and frequency resolution has increased by a factor of 4 compared to the original signal. The lowpass filter output is then filtered once again for further decomposition. This process continues until two samples are left. For this specific example there would be 8 levels of decomposition, each having half the number of samples of the previous level. The DWT of the original signal is then obtained by concatenating all coefficients starting from the last level of decomposition (remaining two samples, in this case). The DWT will then have the same number of coefficients as the original signal.

The frequencies that are most prominent in the original signal will appear as high amplitudes in that region of the DWT signal that includes those particular frequencies. The difference of this transform from the Fourier transform is that the time localization of these frequencies will not be lost. However, the time localization will have a resolution that depends on which level they appear. If the main information of the signal lies in the high frequencies, as happens most often, the time localization of these frequencies will be more precise, since they are characterized by more number of samples. If the main information lies only at very low frequencies, the time localization will not be very precise, since few samples are used to express signal at these frequencies. This procedure in effect offers a good time resolution at high frequencies, and good frequency resolution at low frequencies. Most practical signals encountered are of this type.

The frequency bands that are not very prominent in the original signal will have very low amplitudes, and that part of the DWT signal can be discarded without any major loss of information, allowing data reduction. Figure 4.2 illustrates an example of how DWT signals look like and how data reduction is provided. Figure $4.2_a$ shows a typical 512-sample signal that is normalized to unit amplitude. The horizontal axis is the number of samples, whereas the vertical axis is the normalized amplitude. Figure $4.2_b$ shows the 8 level DWT of the signal in Figure $4.2_a$. The last 256 samples in this signal correspond to the highest frequency band in the signal, the previous 128 samples correspond to the second highest frequency band and so on. It should be noted that only the first 64 samples, which correspond to lower frequencies of the analysis, carry relevant information and the rest of this signal has virtually no information. Therefore, all but the first 64 samples can be discarded without any loss of information. This is how DWT provides a very effective data reduction scheme.

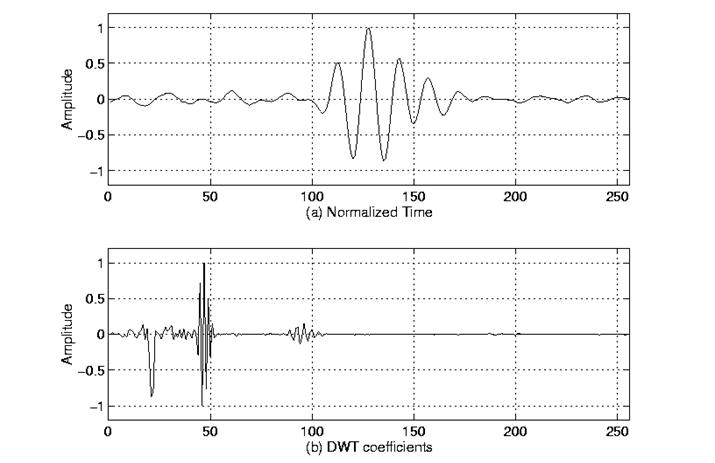
Figure 4.2 Example of a DWT

We will revisit this example, since it provides important insight to how DWT should be interpreted. Before that, however, we need to conclude our mathematical analysis of the DWT.

One important property of the discrete wavelet transform is the relationship between the impulse responses of the highpass and lowpass filters. The highpass and lowpass filters are not independent of each other, and they are related by

$g[L - 1 - n] = (-1)^n \cdot h[n]$

Equation 4.4

where g[n] is the highpass, h[n] is the lowpass filter, and L is the filter length (in number of points). Note that the two filters are odd index alternated reversed versions of each other. Lowpass to highpass conversion is provided by the (-1)n term. Filters satisfying this condition are commonly used in signal processing, and they are known as the Quadrature Mirror Filters (QMF). The two filtering and subsampling operations can be expressed by

$y_{high}[k] = \sum\limits_{n} x[n] \cdot g[-n + 2k]$

$y_{low}[k] = \sum\limits_{n} x[n] \cdot h[-n + 2k]$

Equation 4.5

The reconstruction in this case is very easy since halfband filters form orthonormal bases. The above procedure is followed in reverse order for the reconstruction. The signals at every level are upsampled by two, passed through the synthesis filters g[n], and h[n] (highpass and lowpass, respectively), and then added. The interesting point here is that the analysis and synthesis filters are identical to each other, except for a time reversal. Therefore, the reconstruction formula becomes (for each layer)

$x[n] = \sum\limits_{k = -\infty}^\infty \left( \, y_{high}[k] \cdot g[-n + 2k] \, \right) + \left( \, y_{low}[k] \cdot h[-n + 2k] \, \right)$

Equation 4.6

However, if the filters are not ideal halfband, then perfect reconstruction cannot be achieved. Although it is not possible to realize ideal filters, under certain conditions it is possible to find filters that provide perfect reconstruction. The most famous ones are the ones developed by Ingrid Daubechies, and they are known as Daubechies' wavelets.

Note that due to successive subsampling by 2, the signal length must be a power of 2, or at least a multiple of power of 2, in order this scheme to be efficient. The length of the signal determines the number of levels that the signal can be decomposed to. For example, if the signal length is 1024, ten levels of decomposition are possible.

Interpreting the DWT coefficients can sometimes be rather difficult because the way DWT coefficients are presented is rather peculiar. To make a real long story real short, DWT coefficients of each level are concatenated, starting with the last level. An example is in order to make this concept clear:

Suppose we have a 256-sample long signal sampled at 10 MHZ and we wish to obtain its DWT coefficients. Since the signal is sampled at 10 MHz, the highest frequency component that exists in the signal is 5 MHz. At the first level, the signal is passed through the lowpass filter h[n], and the highpass filter g[n], the outputs of which are subsampled by two. The highpass filter output is the first level DWT coefficients. There are 128 of them, and they represent the signal in the [2.5 5] MHz range. These 128 samples are the last 128 samples plotted. The lowpass filter output, which also has 128 samples, but spanning the frequency band of [0 2.5] MHz, are further decomposed by passing them through the same h[n] and g[n]. The output of the second highpass filter is the level 2 DWT coefficients and these 64 samples precede the 128 level 1 coefficients in the plot. The output of the second lowpass filter is further decomposed, once again by passing it through the filters h[n] and g[n]. The output of the third highpass filter is the level 3 DWT coefficiets. These 32 samples precede the level 2 DWT coefficients in the plot.

The procedure continues until only 1 DWT coefficient can be computed at level 9. This one coefficient is the first to be plotted in the DWT plot. This is followed by 2 level 8 coefficients, 4 level 7 coefficients, 8 level 6 coefficients, 16 level 5 coefficients, 32 level 4 coefficients, 64 level 3 coefficients, 128 level 2 coefficients and finally 256 level 1 coefficients. Note that less and less number of samples is used at lower frequencies, therefore, the time resolution decreases as frequency decreases, but since the frequency interval also decreases at low frequencies, the frequency resolution increases. Obviously, the first few coefficients would not carry a whole lot of information, simply due to greatly reduced time resolution. To illustrate this richly bizarre DWT representation let us take a look at a real world signal. Our original signal is a 256-sample long ultrasonic signal, which was sampled at 25 MHz. This signal was originally generated by using a 2.25 MHz transducer, therefore the main spectral component of the signal is at 2.25 MHz. The last 128 samples correspond to [6.25 12.5] MHz range. As seen from the plot, no information is available here, hence these samples can be discarded without any loss of information. The preceding 64 samples represent the signal in the [3.12 6.25] MHz range, which also does not carry any significant information. The little glitches probably correspond to the high frequency noise in the signal. The preceding 32 samples represent the signal in the [1.5 3.1] MHz range. As you can see, the majority of the signal's energy is focused in these 32 samples, as we expected to see. The previous 16 samples correspond to [0.75 1.5] MHz and the peaks that are seen at this level probably represent the lower frequency envelope of the signal. The previous samples probably do not carry any other significant information. It is safe to say that we can get by with the 3rd and 4th level coefficients, that is we can represent this 256 sample long signal with 16+32=48 samples, a significant data reduction which would make your computer quite happy.

One area that has benefited the most from this particular property of the wavelet transforms is image processing. As you may well know, images, particularly high-resolution images, claim a lot of disk space. As a matter of fact, if this tutorial is taking a long time to download, that is mostly because of the images. DWT can be used to reduce the image size without losing much of the resolution. Here is how:

For a given image, you can compute the DWT of, say each row, and discard all values in the DWT that are less then a certain threshold. We then save only those DWT coefficients that are above the threshold for each row, and when we need to reconstruct the original image, we simply pad each row with as many zeros as the number of discarded coefficients, and use the inverse DWT to reconstruct each row of the original image. We can also analyze the image at different frequency bands, and reconstruct the original image by using only the coefficients that are of a particular band. I will try to put sample images hopefully soon, to illustrate this point.

Another issue that is receiving more and more attention is carrying out the decomposition (subband coding) not only on the lowpass side but on both sides. In other words, zooming into both low and high frequency bands of the signal separately. This can be visualized as having both sides of the tree structure of Figure 4.1. What result is what is known as the wavelet packages. We will not discuss wavelet packages in this here, since it is beyond the scope of this tutorial. Anyone who is interested in wavelet packages, or more information on DWT can find this information in any of the numerous texts available in the market.

And this concludes our mini series of wavelet tutorial. If I could be of any assistance to anyone struggling to understand the wavelets, I would consider the time and the effort that went into this tutorial well spent. I would like to remind that this tutorial is neither a complete nor a through coverage of the wavelet transforms. It is merely an overview of the concept of wavelets and it was intended to serve as a first reference for those who find the available texts on wavelets rather complicated. There might be many structural and/or technical mistakes, and I would appreciate if you could point those out to me. Your feedback is of utmost importance for the success of this tutorial.

Thank you very much for your interest in The Wavelet Tutorial .

All Rights Reserved. This tutorial is intended for educational purposes only. Unauthorized copying, duplicating and publishing is strictly prohibited.

Robi Polikar
Rowan University
Phone: (856) 256 5372
polikar@rowan.edu