Wavelet Tutorial - Part 3
by Robi Polikar
Multiresolution Analysis and the Continuous Wavelet Transform
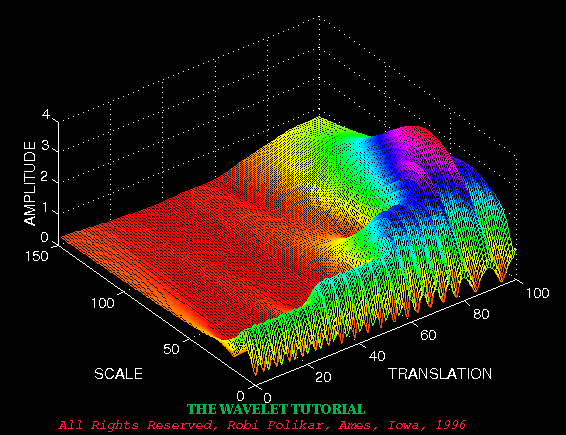
Multiresolution Analysis
Although the time and frequency resolution problems are results of a physical phenomenon (the Heisenberg uncertainty principle) and exist regardless of the transform used, it is possible to analyze any signal by using an alternative approach called the multiresolution analysis (MRA). MRA, as implied by its name, analyzes the signal at different frequencies with different resolutions. Every spectral component is not resolved equally as was the case in the STFT.
MRA is designed to give good time resolution and poor frequency resolution at high frequencies and good frequency resolution and poor time resolution at low frequencies. This approach makes sense especially when the signal at hand has high frequency components for short durations and low frequency components for long durations. Fortunately, the signals that are encountered in practical applications are often of this type. For example, the following shows a signal of this type. It has a relatively low frequency component throughout the entire signal and relatively high frequency components for a short duration somewhere around the middle.
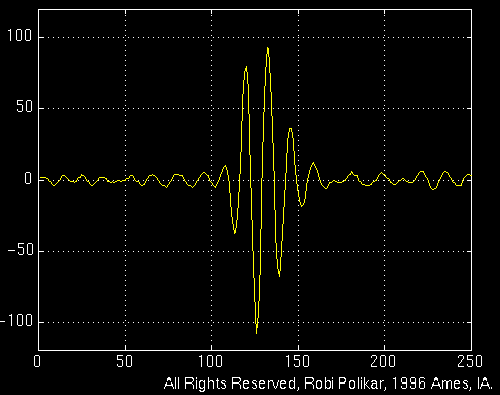
Figure 3.1
The Continuous Wavelet Transform
The continuous wavelet transform was developed as an alternative approach to the short time Fourier transform to overcome the resolution problem. The wavelet analysis is done in a similar way to the STFT analysis, in the sense that the signal is multiplied with a function, {\it the wavelet}, similar to the window function in the STFT, and the transform is computed separately for different segments of the time-domain signal. However, there are two main differences between the STFT and the CWT:
- The Fourier transforms of the windowed signals are not taken, and therefore single peak will be seen corresponding to a sinusoid, i.e., negative frequencies are not computed.
- The width of the window is changed as the transform is computed for every single spectral component, which is probably the most significant characteristic of the wavelet transform.
The continuous wavelet transform is defined as follows
$CWT_x^\psi(\tau,s) = \Psi_x^\psi(\tau,s) = \frac{1}{\sqrt{|s|}} \int x(t) \psi^* \left( \frac{t - \tau}{s} \right) dt$
Equation 3.1
Equation 3.1
As seen in the above equation, the transformed signal is a function of two variables, tau and s, the translation and scale parameters, respectively. $\psi(t)$ is the transforming function, and it is called the mother wavelet. The term mother wavelet gets its name due to two important properties of the wavelet analysis as explained below:
The term wavelet means a small wave. The smallness refers to the condition that this (window) function is of finite length (compactly supported). The wave refers to the condition that this function is oscillatory . The term mother implies that the functions with different region of support that are used in the transformation process are derived from one main function, or the mother wavelet. In other words, the mother wavelet is a prototype for generating the other window functions.
The term translation is used in the same sense as it was used in the STFT; it is related to the location of the window, as the window is shifted through the signal. This term, obviously, corresponds to time information in the transform domain. However, we do not have a frequency parameter, as we had before for the STFT. Instead, we have scale parameter which is defined as $\frac{1}{frequency}$. The term frequency is reserved for the STFT. Scale is described in more detail in the next section.
The Scale
The parameter scale in the wavelet analysis is similar to the scale used in maps. As in the case of maps, high scales correspond to a non-detailed global view (of the signal), and low scales correspond to a detailed view. Similarly, in terms of frequency, low frequencies (high scales) correspond to a global information of a signal (that usually spans the entire signal), whereas high frequencies (low scales) correspond to a detailed information of a hidden pattern in the signal (that usually lasts a relatively short time). Cosine signals corresponding to various scales are given as examples in the following figure .
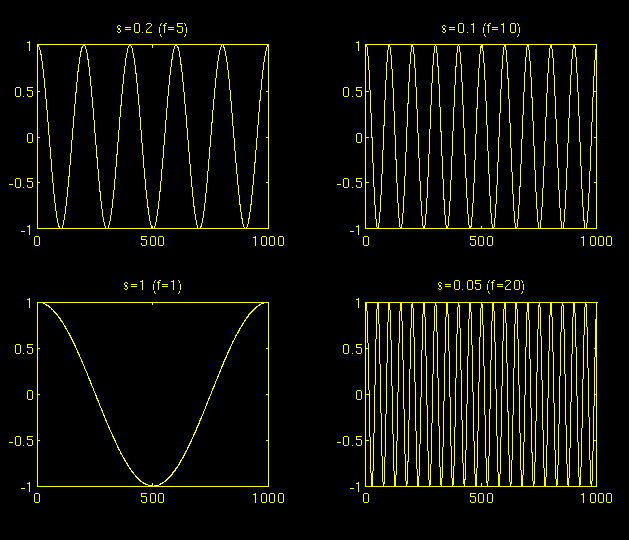
Figure 3.2
Fortunately in practical applications, low scales (high frequencies) do not last for the entire duration of the signal, unlike those shown in the figure, but they usually appear from time to time as short bursts, or spikes. High scales (low frequencies) usually last for the entire duration of the signal.
Scaling, as a mathematical operation, either dilates or compresses a signal. Larger scales correspond to dilated (or stretched out) signals and small scales correspond to compressed signals. All of the signals given in the figure are derived from the same cosine signal, i.e., they are dilated or compressed versions of the same function. In the above figure, s = 0.05 is the smallest scale, and s = 1 is the largest scale.
In terms of mathematical functions, if f(t) is a given function f(st) corresponds to a contracted (compressed) version of f(t) if s > 1 and to an expanded (dilated) version of f(t) if s < 1.
However, in the definition of the wavelet transform, the scaling term is used in the denominator, and therefore, the opposite of the above statements holds, i.e., scales s > 1 dilates the signals whereas scales s < 1 , compresses the signal. This interpretation of scale will be used throughout this text.
Computation of the CWT
Interpretation of the above equation will be explained in this section. Let x(t) is the signal to be analyzed. The mother wavelet is chosen to serve as a prototype for all windows in the process. All the windows that are used are the dilated (or compressed) and shifted versions of the mother wavelet. There are a number of functions that are used for this purpose. The Morlet wavelet and the Mexican hat function are two candidates, and they are used for the wavelet analysis of the examples which are presented later in this chapter.
Once the mother wavelet is chosen the computation starts with s = 1 and the continuous wavelet transform is computed for all values of s , smaller and larger than ``1''. However, depending on the signal, a complete transform is usually not necessary. For all practical purposes, the signals are bandlimited, and therefore, computation of the transform for a limited interval of scales is usually adequate. In this study, some finite interval of values for s were used, as will be described later in this chapter.
For convenience, the procedure will be started from scale s = 1 and will continue for the increasing values of s , i.e., the analysis will start from high frequencies and proceed towards low frequencies. This first value of s will correspond to the most compressed wavelet. As the value of s is increased, the wavelet will dilate.
The wavelet is placed at the beginning of the signal at the point which corresponds to time = 0. The wavelet function at scale ``1'' is multiplied by the signal and then integrated over all times. The result of the integration is then multiplied by the constant number $\frac{1}{\sqrt{s}}$. This multiplication is for energy normalization purposes so that the transformed signal will have the same energy at every scale. The final result is the value of the transformation, i.e., the value of the continuous wavelet transform at time zero and scale s = 1 . In other words, it is the value that corresponds to the point $\boldsymbol \tau$ = 0 , s = 1 in the time-scale plane.
The wavelet at scale s = 1 is then shifted towards the right by $\tau$ amount to the location t = $\boldsymbol \tau$ , and the above equation is computed to get the transform value at t = tau, s = 1 in the time-frequency plane.
This procedure is repeated until the wavelet reaches the end of the signal. One row of points on the time-scale plane for the scale s = 1 is now completed.
Then, s is increased by a small value. Note that, this is a continuous transform, and therefore, both $\boldsymbol \tau$ and s must be incremented continuously . However, if this transform needs to be computed by a computer, then both parameters are increased by a sufficiently small step size. This corresponds to sampling the time-scale plane.
The above procedure is repeated for every value of s. Every computation for a given value of s fills the corresponding single row of the time-scale plane. When the process is completed for all desired values of s, the CWT of the signal has been calculated.
The figures below illustrate the entire process step by step.
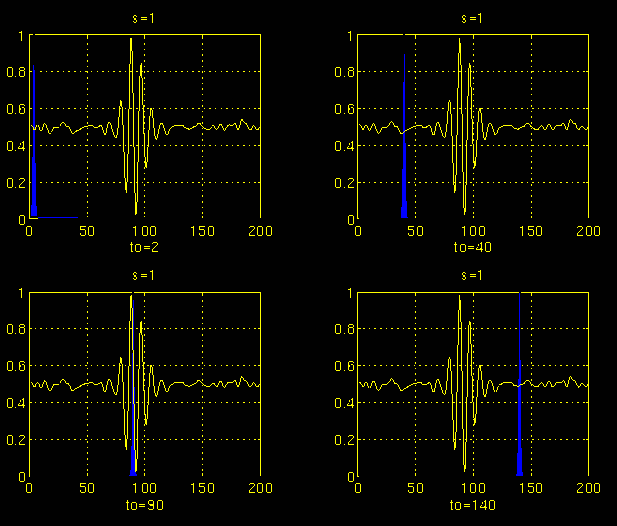
Figure 3.3
In Figure 3.3, the signal and the wavelet function are shown for four different values of $\boldsymbol \tau$. The signal is a truncated version of the signal shown in Figure 3.1. The scale value is 1 , corresponding to the lowest scale, or highest frequency. Note how compact it is (the blue window). It should be as narrow as the highest frequency component that exists in the signal. Four distinct locations of the wavelet function are shown in the figure at $\boldsymbol {t_o}$ = 2 , $\boldsymbol {t_o}$ = 40, $\boldsymbol {t_o}$ = 90, and $\boldsymbol {t_o}$ = 140 . At every location, it is multiplied by the signal. Obviously, the product is nonzero only where the signal falls in the region of support of the wavelet, and it is zero elsewhere. By shifting the wavelet in time, the signal is localized in time, and by changing the value of s , the signal is localized in scale (frequency).
If the signal has a spectral component that corresponds to the current value of s (which is 1 in this case), the product of the wavelet with the signal at the location where this spectral component exists gives a relatively large value. If the spectral component that corresponds to the current value of s is not present in the signal, the product value will be relatively small, or zero. The signal in Figure 3.3 has spectral components comparable to the window's width at s = 1 around t = 100 ms.
The continuous wavelet transform of the signal in Figure 3.3 will yield large values for low scales around time 100 ms, and small values elsewhere. For high scales, on the other hand, the continuous wavelet transform will give large values for almost the entire duration of the signal, since low frequencies exist at all times.
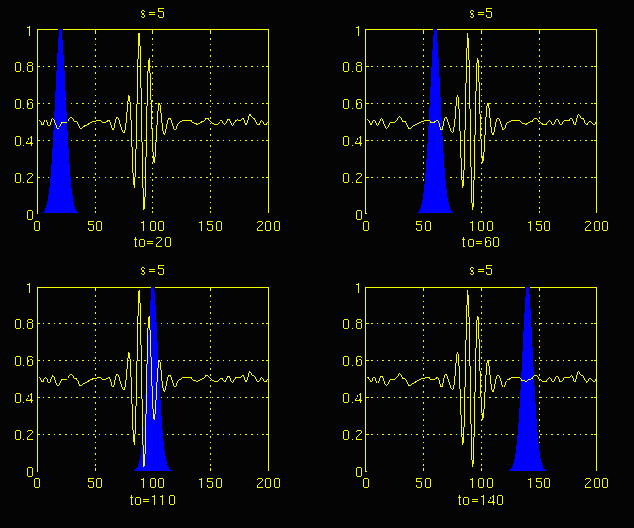
Figure 3.4
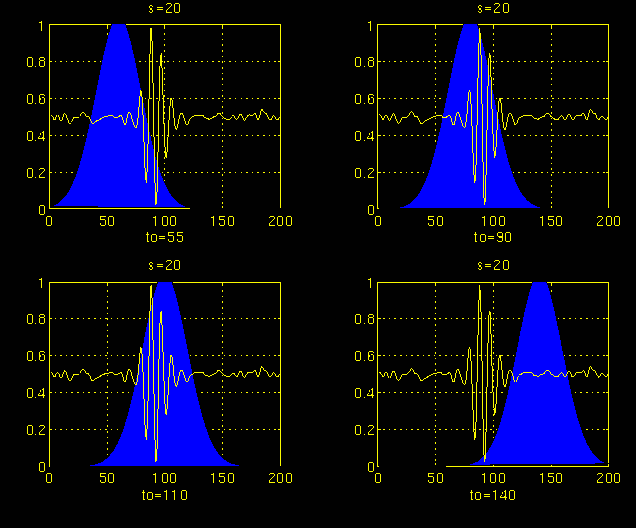
Figure 3.5
Figures 3.4 and 3.5 illustrate the same process for the scales s = 5 and s = 20, respectively. Note how the window width changes with increasing scale (decreasing frequency). As the window width increases, the transform starts picking up the lower frequency components.
As a result, for every scale and for every time (interval), one point of the time-scale plane is computed. The computations at one scale construct the rows of the time-scale plane, and the computations at different scales construct the columns of the time-scale plane.
Now, let's take a look at an example, and see how the wavelet transform really looks like. Consider the non-stationary signal in Figure 3.6. This is similar to the example given for the STFT, except at different frequencies. As stated on the figure, the signal is composed of four frequency components at 30 Hz, 20 Hz, 10 Hz and 5 Hz.
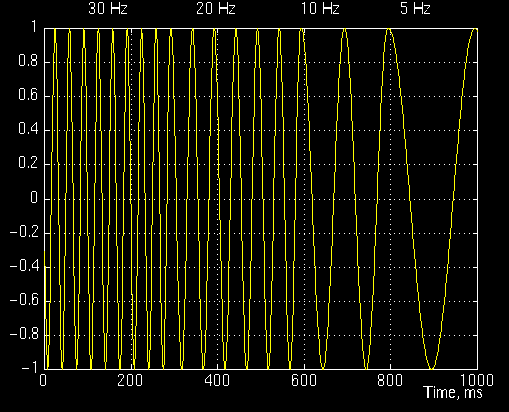
Figure 3.6
Figure 3.7 is the continuous wavelet transform (CWT) of this signal. Note that the axes are translation and scale, not time and frequency. However, translation is strictly related to time, since it indicates where the mother wavelet is located. The translation of the mother wavelet can be thought of as the time elapsed since t = 0 . The scale, however, has a whole different story. Remember that the scale parameter s in equation 3.1 is actually inverse of frequency. In other words, whatever we said about the properties of the wavelet transform regarding the frequency resolution, inverse of it will appear on the figures showing the WT of the time-domain signal.
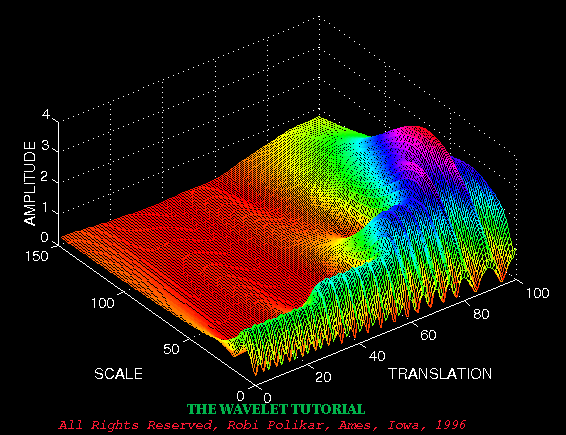
Figure 3.7
Note that in Figure 3.7 that smaller scales correspond to higher frequencies, i.e., frequency decreases as scale increases, therefore, that portion of the graph with scales around zero, actually correspond to highest frequencies in the analysis, and that with high scales correspond to lowest frequencies. Remember that the signal had 30 Hz (highest frequency) components first, and this appears at the lowest scale at a translations of 0 to 30. Then comes the 20 Hz component, second highest frequency, and so on. The 5 Hz component appears at the end of the translation axis (as expected), and at higher scales (lower frequencies) again as expected.
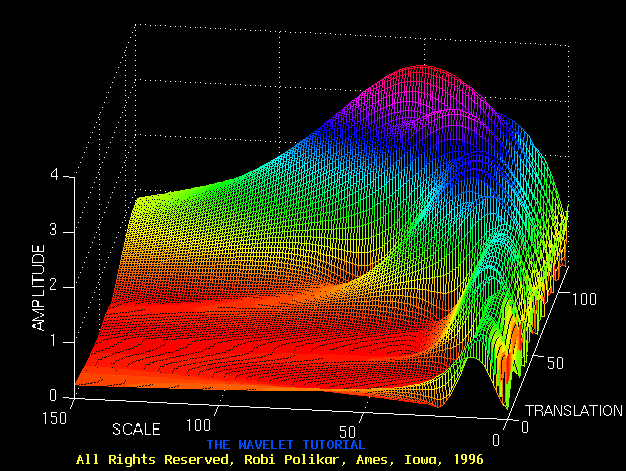
Figure 3.8
Now, recall these resolution properties: Unlike the STFT which has a constant resolution at all times and frequencies, the WT has a good time and poor frequency resolution at high frequencies, and good frequency and poor time resolution at low frequencies. Figure 3.8 shows the same WT in Figure 3.7 from another angle to better illustrate the resolution properties: In Figure 3.8, lower scales (higher frequencies) have better scale resolution (narrower in scale, which means that it is less ambiguous what the exact value of the scale) which correspond to poorer frequency resolution . Similarly, higher scales have scale frequency resolution (wider support in scale, which means it is more ambitious what the exact value of the scale is) , which correspond to better frequency resolution of lower frequencies.
The axes in Figure 3.7 and 3.8 are normalized and should be evaluated accordingly. Roughly speaking the 100 points in the translation axis correspond to 1000 ms, and the 150 points on the scale axis correspond to a frequency band of 40 Hz (the numbers on the translation and scale axis do not correspond to seconds and Hz, respectively , they are just the number of samples in the computation).
Time and Frequency Resolutions
In this section we will take a closer look at the resolution properties of the wavelet transform. Remember that the resolution problem was the main reason why we switched from STFT to WT.
The illustration in Figure 3.9 is commonly used to explain how time and frequency resolutions should be interpreted. Every box in Figure 3.9 corresponds to a value of the wavelet transform in the time-frequency plane. Note that boxes have a certain non-zero area, which implies that the value of a particular point in the time-frequency plane cannot be known. All the points in the time-frequency plane that falls into a box is represented by one value of the WT.
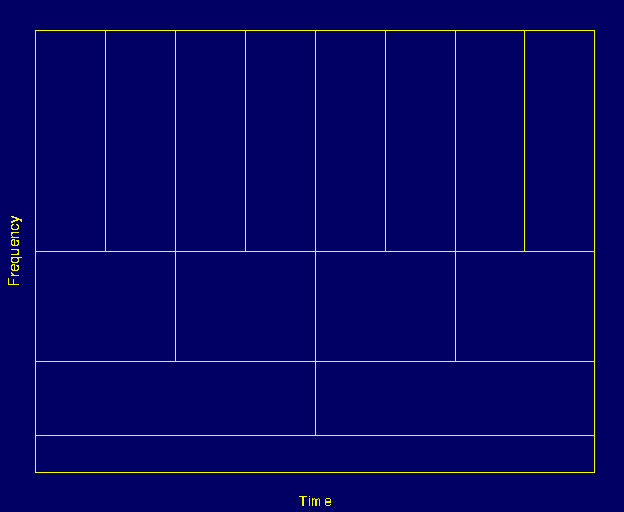
Figure 3.9
Let's take a closer look at Figure 3.9: First thing to notice is that although the widths and heights of the boxes change, the area is constant. That is each box represents an equal portion of the time-frequency plane, but giving different proportions to time and frequency. Note that at low frequencies, the height of the boxes are shorter (which corresponds to better frequency resolutions, since there is less ambiguity regarding the value of the exact frequency), but their widths are longer (which correspond to poor time resolution, since there is more ambiguity regarding the value of the exact time). At higher frequencies the width of the boxes decreases, i.e., the time resolution gets better, and the heights of the boxes increase, i.e., the frequency resolution gets poorer.
Before concluding this section, it is worthwhile to mention how the partition looks like in the case of STFT. Recall that in STFT the time and frequency resolutions are determined by the width of the analysis window, which is selected once for the entire analysis, i.e., both time and frequency resolutions are constant. Therefore the time-frequency plane consists of squares in the STFT case.
Regardless of the dimensions of the boxes, the areas of all boxes, both in STFT and WT, are the same and determined by Heisenberg's inequality . As a summary, the area of a box is fixed for each window function (STFT) or mother wavelet (CWT), whereas different windows or mother wavelets can result in different areas. However, all areas are lower bounded by $\boldsymbol {\frac{1}{4} \pi}$. That is, we cannot reduce the areas of the boxes as much as we want due to the Heisenberg's uncertainty principle. On the other hand, for a given mother wavelet the dimensions of the boxes can be changed, while keeping the area the same. This is exactly what wavelet transform does.
The Wavelet Theory: A Mathematical Approach
This section describes the main idea of wavelet analysis theory, which can also be considered to be the underlying concept of most of the signal analysis techniques. The FT defined by Fourier use basis functions to analyze and reconstruct a function. Every vector in a vector space can be written as a linear combination of the basis vectors in that vector space , i.e., by multiplying the vectors by some constant numbers, and then by taking the summation of the products. The analysis of the signal involves the estimation of these constant numbers (transform coefficients, or Fourier coefficients, wavelet coefficients, etc). The synthesis, or the reconstruction, corresponds to computing the linear combination equation.
All the definitions and theorems related to this subject can be found in Keiser's book, A Friendly Guide to Wavelets but an introductory level knowledge of how basis functions work is necessary to understand the underlying principles of the wavelet theory. Therefore, this information will be presented in this section.
Basis Vectors
Note: Most of the equations include letters of the Greek alphabet. These letters are written out explicitly in the text with their names, such as tau, psi, phi etc. For capital letters, the first letter of the name has been capitalized, such as, Tau, Psi, Phi etc. Also, subscripts are shown by the underscore character _ , and superscripts are shown by the ^ character. Also note that all letters or letter names written in bold type face represent vectors, Some important points are also written in bold face, but the meaning should be clear from the context.
A basis of a vector space V is a set of linearly independent vectors, such that any vector v in V can be written as a linear combination of these basis vectors. There may be more than one basis for a vector space. However, all of them have the same number of vectors, and this number is known as the dimension of the vector space. For example in two-dimensional space, the basis will have two vectors.
$v = \sum\limits_{k} \nu^k b_k$
Equation 3.2
Equation 3.2
Equation 3.2 shows how any vector v can be written as a linear combination of the basis vectors $\boldsymbol {b_k}$ and the corresponding coefficients $\boldsymbol {\nu^k}$.
This concept, given in terms of vectors, can easily be generalized to functions, by replacing the basis vectors $\boldsymbol {b_k}$ with basis functions $\boldsymbol {\phi_k(t)}$, and the vector v with a function f(t). Equation 3.2 then becomes
$f(t) = \sum\limits_{k} \mu_k \phi_k (t)$
Equation $3.2_a$
Equation $3.2_a$
The complex exponential (sines and cosines) functions are the basis functions for the FT. Furthermore, they are orthogonal functions, which provide some desirable properties for reconstruction.
Let f(t) and g(t) be two functions in $L^2 [a,b]$. ($L^2 [a,b]$ denotes the set of square integrable functions in the interval $[a,b]$). The inner product of two functions is defined by Equation 3.3:
$< f(t), g(t) > = \int_a^b f(t) \cdot g^*(t) dt$
Equation 3.3
Equation 3.3
According to the above definition of the inner product, the CWT can be thought of as the inner product of the test signal with the basis functions $\psi_(\tau ,s)(t)$:
$CWT_x^\psi(\tau, s) = \Psi_x^\psi(\tau, s) = \int x(t) \cdot \psi^*_{\tau, s}(t) dt$
Equation 3.4
Equation 3.4
where,
$\psi_{\tau, s} = \frac{1}{\sqrt{s}} \psi \left( \frac{t - \tau}{s} \right)$
Equation 3.5
Equation 3.5
This definition of the CWT shows that the wavelet analysis is a measure of similarity between the basis functions (wavelets) and the signal itself. Here the similarity is in the sense of similar frequency content. The calculated CWT coefficients refer to the closeness of the signal to the wavelet at the current scale .
This further clarifies the previous discussion on the correlation of the signal with the wavelet at a certain scale. If the signal has a major component of the frequency corresponding to the current scale, then the wavelet (the basis function) at the current scale will be similar or close to the signal at the particular location where this frequency component occurs. Therefore, the CWT coefficient computed at this point in the time-scale plane will be a relatively large number.
Inner Products, Orthogonality, and Orthonormality
Two vectors v , w are said to be orthogonal if their inner product equals zero
$< v, w > = \sum\limits_{n} v_n w^*_n = 0$
Equation 3.6
Equation 3.6
Similarly, two functions $f$ and $g$ are said to be orthogonal to each other if their inner product is zero:
$< f(t), g(t) > = \int_a^b f(t) \cdot g^*(t) \cdot dt = 0$
Equation 3.7
Equation 3.7
A set of vectors {$\boldsymbol{v_1, v_2, ....,v_n}$} is said to be orthonormal , if they are pairwise orthogonal to each other, and all have length "1". This can be expressed as:
$< v_m, v_n > = \delta_{mn}$
Equation 3.8
Equation 3.8
Similarly, a set of functions {$phi_k(t)$}, $k=1,2,3,...,$ is said to be orthonormal if
$\int_a^b \phi_k(t) \cdot \phi^*_l(t) \cdot dt = 0$ $k \neq l$ (orthogonality cond.)
Equation 3.9
Equation 3.9
and
$\int_a^b \{ | \phi_k(t) | \}^2 dx = 1$
Equation 3.10
Equation 3.10
or equivalently
$\int_a^b \phi_k(t) \cdot \phi_l^*(t) \cdot dt = \delta_{kl}$
Equation 3.11
Equation 3.11
where, $\delta_{kl}$ is the Kronecker delta function, defined as:
$\delta_{kl} =
\left\{
\begin{array}{ll}
1, & k = l \\
0, & k \neq l\\
\end{array}
\right.$
Equation 3.12
Equation 3.12
As stated above, there may be more than one set of basis functions (or vectors). Among them, the orthonormal basis functions (or vectors) are of particular importance because of the nice properties they provide in finding these analysis coefficients. The orthonormal bases allow computation of these coefficients in a very simple and straightforward way using the orthonormality property.
For orthonormal bases, the coefficients, $\mu_k$, can be calculated as
$\mu_k = < f, \phi_k > = \int f(t) \cdot \phi_k^*(t) \cdot dt$
Equation 3.13
Equation 3.13
and the function f(t) can then be reconstructed by Equation $3.2_a$ by substituting the $\mu_k$ coefficients. This yields
$f(t) = \sum\limits_{k} \mu_k \phi_k(t) = \sum\nolimits_{k} < f, \phi_k > \phi_k(t)$
Equation 3.14
Equation 3.14
Orthonormal bases may not be available for every type of application where a generalized version, biorthogonal bases can be used. The term "biorthogonal" refers to two different bases which are orthogonal to each other, but each do not form an orthogonal set.
In some applications, however, biorthogonal bases also may not be available in which case frames can be used. Frames constitute an important part of wavelet theory, and interested readers are referred to Kaiser's book mentioned earlier.
Following the same order as in chapter 2 for the STFT, some examples of continuous wavelet transform are presented next. The figures given in the examples were generated by a program written to compute the CWT.
Before we close this section, I would like to include two mother wavelets commonly used in wavelet analysis. The Mexican Hat wavelet is defined as the second derivative of the Gaussian function:
$w(t) = \frac{1}{\sqrt{2\pi} \cdot \sigma} e^{\frac{-t^2}{2 \sigma^2}}$
Equation 3.15
Equation 3.15
which is
$\psi(t) = \frac{1}{\sqrt{2 \pi} \cdot \sigma^3} \left( e^{\frac{-t^2}{2 \sigma^2}} \cdot \left( \frac{t^2}{\sigma^2} - 1 \right) \right)$
Equation 3.16
Equation 3.16
The Morlet wavelet is defined as
$w(t) = e^{i a t} \cdot e^{-\frac{t^2}{2\sigma}}$
Equation $3.16_a$
Equation $3.16_a$
where a is a modulation parameter, and sigma is the scaling parameter that affects the width of the window.
Examples
All of the examples that are given below correspond to real-life non-stationary signals. These signals are drawn from a database signals that includes event related potentials of normal people, and patients with Alzheimer's disease. Since these are not test signals like simple sinusoids, it is not as easy to interpret them. They are shown here only to give an idea of how real-life CWTs look like.
The following signal shown in Figure 3.11 belongs to a normal person.
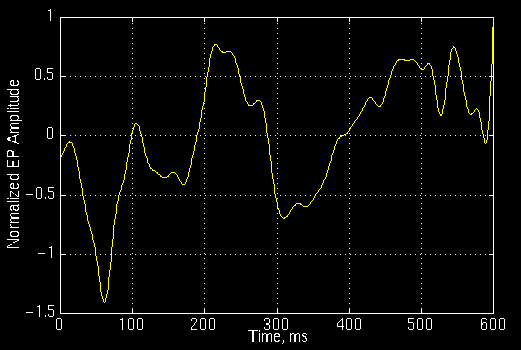
Figure 3.11
and the following is its CWT. The numbers on the axes are of no importance to us. those numbers simply show that the CWT was computed at 350 translation and 60 scale locations on the translation-scale plane. The important point to note here is the fact that the computation is not a true continuous WT, as it is apparent from the computation at finite number of locations. This is only a discretized version of the CWT, which is explained later on this page. Note, however, that this is NOT discrete wavelet transform (DWT) which is the topic of Part IV of this tutorial.
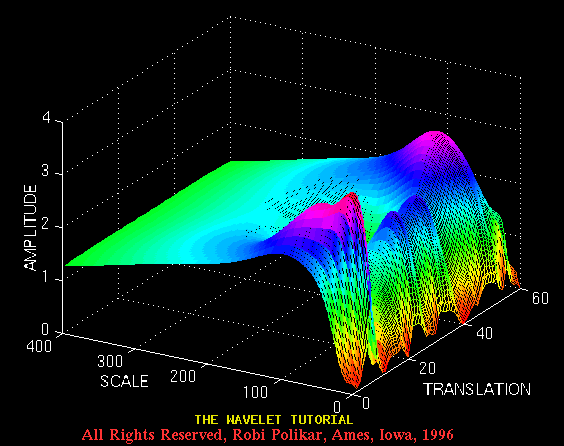
Figure 3.12
and the Figure 3.13 plots the same transform from a different angle for better visualization.
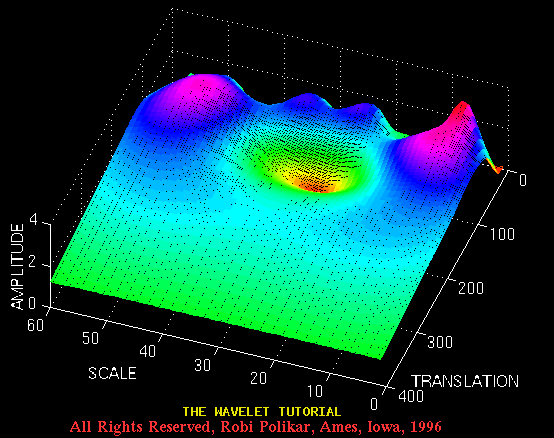
Figure 3.13
Figure 3.14 plots an event related potential of a patient diagnosed with Alzheimer's disease
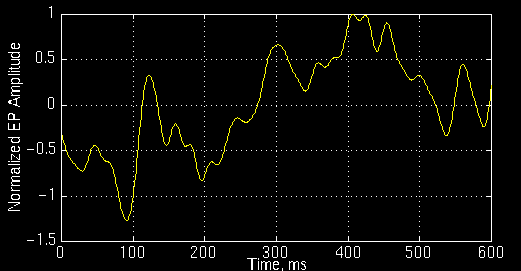
Figure 3.14
and Figure 3.15 illustrates its CWT:
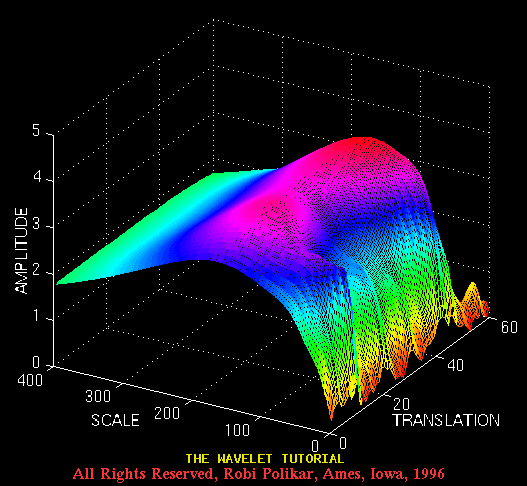
Figure 3.15
and here is another view from a different angle
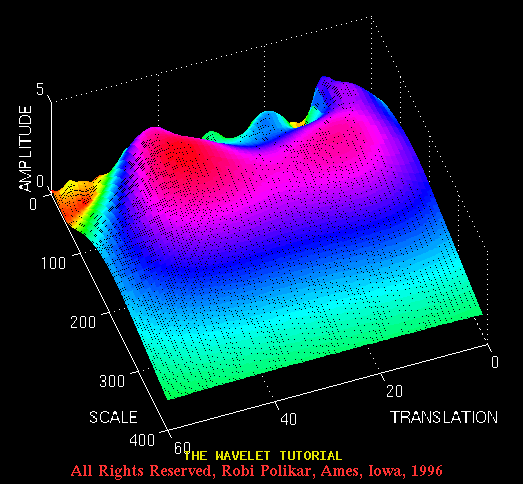
Figure 3.16
The Wavelet Synthesis
The continuous wavelet transform is a reversible transform, provided that Equation 3.18 is satisfied. Fortunately, this is a very non-restrictive requirement. The continuous wavelet transform is reversible if Equation 3.18 is satisfied, even though the basis functions are in general may not be orthonormal. The reconstruction is possible by using the following reconstruction formula:
$x(t) = \frac{1}{C_\psi^2} \int_s \int_\tau \left[ \Psi^\psi_x(\tau, s) \frac{1}{s^2} \psi \left( \frac{t - \tau}{s} \right) \right] d\tau \cdot ds$
Equation 3.17
Equation 3.17
where $C_\psi$ is a constant that depends on the wavelet used. The success of the reconstruction depends on this constant called, the admissibility constant , to satisfy the following admissibility condition :
$C_\psi = \left\{ 2 \pi \int_{-\infty}^{\infty} \frac{|\hat{\psi}(\xi)|^2}{|\zeta|} d\xi \right\} ^{\frac{1}{2}} < \infty$
Equation 3.18
Equation 3.18
where $\hat{\psi}(\xi)$ is the FT of $\psi(t)$. Equation 3.18 implies that $\hat{\psi}(0) = 0$, which is
$\int \psi(t) \cdot dt = 0$
Equation 3.19
Equation 3.19
As stated above, Equation 3.19 is not a very restrictive requirement since many wavelet functions can be found whose integral is zero. For Equation 3.19 to be satisfied, the wavelet must be oscillatory.
Discretization of the Continuous Wavelet Transform: The Wavelet Series
In today's world, computers are used to do most computations (well,...ok... almost all computations). It is apparent that neither the FT, nor the STFT, nor the CWT can be practically computed by using analytical equations, integrals, etc. It is therefore necessary to discretize the transforms. As in the FT and STFT, the most intuitive way of doing this is simply sampling the time-frequency (scale) plane. Again intuitively, sampling the plane with a uniform sampling rate sounds like the most natural choice. However, in the case of WT, the scale change can be used to reduce the sampling rate.
At higher scales (lower frequencies), the sampling rate can be decreased, according to Nyquist's rule. In other words, if the time-scale plane needs to be sampled with a sampling rate of $\boldsymbol{N_1}$ at scale $\boldsymbol{s_1}$, the same plane can be sampled with a sampling rate of $\boldsymbol{N_2}$, at scale $\boldsymbol{s_2}$, where, $\boldsymbol{s_1 < s_2}$ (corresponding to frequencies $\boldsymbol{f_1 > f_2}$ ) and $\boldsymbol{N_2 < N_1}$. The actual relationship between $\boldsymbol{N_1}$ and $\boldsymbol{N_2}$ is
$N_2 = \frac{s_1}{s_2} N_1$
Equation 3.20
Equation 3.20
or
$N_2 = \frac{f_2}{f_1} N_1$
Equation 3.21
Equation 3.21
In other words, at lower frequencies the sampling rate can be decreased which will save a considerable amount of computation time.
It should be noted at this time, however, that the discretization can be done in any way without any restriction as far as the analysis of the signal is concerned. If synthesis is not required, even the Nyquist criteria does not need to be satisfied. The restrictions on the discretization and the sampling rate become important if, and only if, the signal reconstruction is desired. Nyquist's sampling rate is the minimum sampling rate that allows the original continuous time signal to be reconstructed from its discrete samples. The basis vectors that are mentioned earlier are of particular importance for this reason.
As mentioned earlier, the wavelet $\boldsymbol{\psi(\tau,s)}$ satisfying Equation 3.18, allows reconstruction of the signal by Equation 3.17. However, this is true for the continuous transform. The question is: can we still reconstruct the signal if we discretize the time and scale parameters? The answer is "yes", under certain conditions (as they always say in commercials: certain restrictions apply !!!).
The scale parameter s is discretized first on a logarithmic grid. The time parameter is then discretized with respect to the scale parameter , i.e., a different sampling rate is used for every scale. In other words, the sampling is done on the dyadic sampling grid shown in Figure 3.17 :

Figure 3.17
Think of the area covered by the axes as the entire time-scale plane. The CWT assigns a value to the continuum of points on this plane. Therefore, there are an infinite number of CWT coefficients. First consider the discretization of the scale axis. Among that infinite number of points, only a finite number are taken, using a logarithmic rule. The base of the logarithm depends on the user. The most common value is 2 because of its convenience. If 2 is chosen, only the scales 2, 4, 8, 16, 32, 64,...etc. are computed. If the value was 3, the scales 3, 9, 27, 81, 243,...etc. would have been computed. The time axis is then discretized according to the discretization of the scale axis. Since the discrete scale changes by factors of 2 , the sampling rate is reduced for the time axis by a factor of 2 at every scale.
Note that at the lowest scale (s = 2), only 32 points of the time axis are sampled (for the particular case given in Figure 3.17). At the next scale value, s = 4, the sampling rate of time axis is reduced by a factor of 2 since the scale is increased by a factor of 2, and therefore, only 16 samples are taken. At the next step, s = 8 and 8 samples are taken in time, and so on.
Although it is called the time-scale plane, it is more accurate to call it the translation-scale plane, because "time" in the transform domain actually corresponds to the shifting of the wavelet in time. For the wavelet series, the actual time is still continuous.
Similar to the relationship between continuous Fourier transform, Fourier series and the discrete Fourier transform, there is a continuous wavelet transform, a semi-discrete wavelet transform (also known as wavelet series) and a discrete wavelet transform.
Expressing the above discretization procedure in mathematical terms, the scale discretization is $\boldsymbol{s = s_0^j}$, and translation discretization is $\boldsymbol{\tau = k \cdot s_0^j \cdot \tau_0}$ where $\boldsymbol{s_0>1}$ and $\boldsymbol{tau_0>0}$. Note, how the translation discretization is dependent on scale discretization with $\boldsymbol{s_0}$.
The continuous wavelet function
$\psi_{\tau, s} = \frac{1}{\sqrt{s}} \psi \left( \frac{t - \tau}{s} \right)$
Equation 3.22
Equation 3.22
$\psi_{j, k}(t) = s_0^{\frac{-j}{2}} \psi \left( s_0^{-j} - k \tau_0 \right)$
Equation 3.23
Equation 3.23
by inserting $\boldsymbol{s = s_0^{\, j}}$, and $\boldsymbol{\tau = k \cdot s_0^{\, j} \cdot \tau_0}$.
If $\boldsymbol{ \left\{ \psi_{(j, \, k)} \right\} }$ constitutes an orthonormal basis, the wavelet series transform becomes
$\Psi^{\psi_{\, j,k}}_x = \int x(t) \, \psi^*_{j, \, k}(t) \, dt$
Equation 3.24
Equation 3.24
or
$x(t) = c_\psi \sum\limits_{j} \sum\limits_{k} \Psi^{\psi_{\, j,k}}_x \, \psi_{\, j,k} (t)$
Equation 3.25
Equation 3.25
A wavelet series requires that $\boldsymbol{ {\psi_{(j, \, k)}} }$ are either orthonormal, biorthogonal, or frame. If $\boldsymbol{ {\psi_{(j,k)}} }$ are not orthonormal, Equation 3.24 becomes
$\Psi^{\psi_{\, j,k}}_x = \int x(t) \, \hat{\psi^*_{(j, \, k)}(t)} \, dt$
Equation 3.26
Equation 3.26
where $\boldsymbol{\hat{\psi_{j, \, k}^*(t)}}$, is either the dual biorthogonal basis or dual frame (Note that * denotes the conjugate).
If $\boldsymbol{ \{ \psi_{(j, \, k)} \} }$ are orthonormal or biorthogonal, the transform will be non-redundant, where as if they form a frame, the transform will be redundant. On the other hand, it is much easier to find frames than it is to find orthonormal or biorthogonal bases.
The following analogy may clear this concept. Consider the whole process as looking at a particular object. The human eyes first determine the coarse view which depends on the distance of the eyes to the object. This corresponds to adjusting the scale parameter $\boldsymbol{s_0^{-j}}$. When looking at a very close object, with great detail, j is negative and large (low scale, high frequency, analyses the detail in the signal). Moving the head (or eyes) very slowly and with very small increments (of angle, of distance, depending on the object that is being viewed), corresponds to small values of $\boldsymbol{\tau = k \cdot s_0^{\, j} \cdot \tau_0}$. Note that when j is negative and large, it corresponds to small changes in time, $\boldsymbol{\tau}$, (high sampling rate) and large changes in $\boldsymbol{s_0^{\, j}}$ (low scale, high frequencies, where the sampling rate is high). The scale parameter can be thought of as magnification too.
How low can the sampling rate be and still allow reconstruction of the signal? This is the main question to be answered to optimize the procedure. The most convenient value (in terms of programming) is found to be "2" for $s_0$ and "1" for $\tau$. Obviously, when the sampling rate is forced to be as low as possible, the number of available orthonormal wavelets is also reduced.
The continuous wavelet transform examples that were given in this chapter were actually the wavelet series of the given signals. The parameters were chosen depending on the signal. Since the reconstruction was not needed, the sampling rates were sometimes far below the critical value where $s_0$ varied from 2 to 10, and $\tau_0$ varied from 2 to 8, for different examples.
This concludes Part III of this tutorial. I hope you now have a basic understanding of what the wavelet transform is all about. There is one thing left to be discussed however. Even though the discretized wavelet transform can be computed on a computer, this computation may take anywhere from a couple seconds to couple hours depending on your signal size and the resolution you want. An amazingly fast algorithm is actually available to compute the wavelet transform of a signal. The discrete wavelet transform (DWT) is introduced in the final chapter of this tutorial, in Part IV.
Let's meet at the grand finale, shall we?
All Rights Reserved. This tutorial is intended for educational purposes only. Unauthorized copying, duplicating and publishing is strictly prohibited.
Robi Polikar
Rowan University
Phone: (856) 256 5372
polikar@rowan.edu