Digital
Image Processing
Course Nos. ECE.09.452 and ECE.09.552
Lab
Project 2: Spatial and Spectral Filtering
This
laboratory has three parts. In parts 1 and 2, you will experiment with the
characteristics of the Fourier transform (both continuous and discrete) of a
digital image. In part 3, you will develop both spatial domain and spectral
domain filters for image enhancement.
Part 1: Continuous
Fourier Transform and Discrete Fourier Transform of Images
Objective
The
objective of this part is to model a simple image template both as a
continuous-space function and as a discrete-space function and analytically
determine its properties in the spatial and spatial frequency domains.
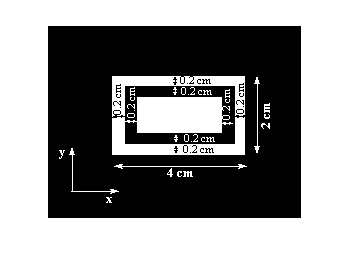
Figure 1: Image for Part 1 (DO NOT download this image! You are required to model it!).
- Model the image shown in
Figure 1 as a continuous-space 2-D function; and plot.
- Obtain, analytically,
the Fourier transform of the continuous-space image; and plot.
- Based on your
observations of the spatial frequency components of the image; determine
the maximum sampling interval (delta_x = delta_y) / minimum sampling spatial frequency, that
will allow reconstruction of the original continuous-space 2-D
function / image.
- Attempt to reconstruct
the original continuous-space function from its samples, either by:
- Convolving the spatial
domain samples with the appropriate Sinc
function (difficult), or
- Windowing the
continuous Fourier transform and taking the inverse discrete Fourier
transform (easier).
Compare with the original discrete-space sequence. Comment
on your results.
- What is the maximum
sampling interval / minimum sampling frequency that will allow
reconstruction of the the discrete-space
image from its Discrete Fourier Transform, that adequately
represents the original continuous-space image?
Part 2: Using the
DFT to compute Spectral Components
- Consider a 2-D function f(x,y) = sin(2*p*fx*x) + sin(2*p*fy*y) where fx
and fy are the
spatial frequencies along the x-
and y-directions respectively. A
digital image is generated by computing this 2-D function over a spatial
range 0 <= x <= S; 0 <=y <=S, such that the range is
divided into N equal points along both the x- and y-directions.
- Generate a sample image by choosing S = 1 cm, N = 128, fx = 30
per and fy = 50 per cm.
- Compute the 2-D DFT of this image. Generate a
surface-plot (>> surf) of its amplitude spectrum with the
axes correctly indicating the spatial frequencies.
- Obtain an image of the amplitude spectrum.
- Vary the parameters S, N, fx ,
and fy. Comment on your results.
Part 3: Spatial and
Spectral Filtering
Objective
The
objective of this part is to study the effects of low-pass and high-pass
filtering an image, using spatial domain and spatial-frequency domain
techniques. You will exercise these techniques on two images: a modeled zone
plate image and a downloaded Moon image.
- Model the zone-plate
image shown in Figure 2(a) as described in Equation 3.75 in the textbook
on page 213, Example 3.23. The image is of size 597 x 597 pixels and is
described by the equation:
z(x,y) = 0.5*(1+cos(x^2
+ y^2));
for x and y varying in the
range [-8.2, 8.2] in steps of 0.0275, and all pixels greater than a distance of
8.2 from the image center set to 0.

Figure 2(a): Zone plate image (DO NOT
download this image! You are required to model it!).
2. Model the zone-plate image
shown in Figure 2(a) as described in Equation 3.75 in the textbook on page 213,
Example 3.23. The image is of size 597 x 597 pixels and is described by the
equation:
z(x,y) = 0.5*(1+cos(x^2
+ y^2));
for x and y varying in the
range [-8.2, 8.2] in steps of 0.0275, and all pixels greater than a distance of
8.2 from the image center set to 0.
3. Generate spatial filtering
masks for lowpass, highpass,
bandreject and bandpass
filters as described in Table 3.7 of the textbook on page 213.
4. Exercise these spatial
filtering masks on the modeled zone plate image and replicate the results shown
in Figure 3.61.
5. Repeat the experiment by
modeling the filters in the spectral domain and attempt to obtain similar
results.
6. Download the image of the
Moon's surface obtained by the Ranger Missions that is
shown in Figure 2(b).
Figure 2 (b): Moon image for Part 3.
7. Generate a 3 x 3 spatial
averaging filter and perform a neighborhood averaging over the original Moon
image. Plot and observe the Fourier spectrum of the averaged image; compare
with the Fourier spectrum of the original image. Comment on your results.
8. Corrupt the original Moon
image with a zero-mean Gaussian noise, so that the SNR of the noisy image is 5 dB. Attempt to minimize noise effects by using appropriate
filters in
- spatial domain, and
- spectral domain.
Indicate the cut-off frequency of the spectral domain
filter. Comment on your results.
9. Corrupt the original Moon
image with impulse (Salt and Pepper) noise of density 0.01. Attempt to minimize
noise effects by using an appropriate spatial domain filter. Comment on your
results.
10. Attempt to generate an image
that contains only the edges of the lunar craters, by high-pass filtering the
original Moon image. Do this using filters in both
- spatial, and
- spectral domains.
Is this possible? What cut-off frequency does the best job?
Comment on your results.
NOTE:
For all
results obtained using spectral domain filters, you must provide images of
- the frequency response of the filter,
- the image spectra before
and after filtering.
Your
report should be in the usual format.